What Is Standard Deviation and Why Is It Important?

Standard deviation is one of the most essential concepts in statistics, providing a measure of how data points differ from the average or mean of a dataset. This concept may seem a bit abstract at first, but its applications are widespread, from quality control in manufacturing to investment analysis in finance. Understanding standard deviation can help us make sense of data variability and uncover insights that are otherwise hard to grasp. In this article, we'll dive into what standard deviation is, how it's calculated, and why it plays such a critical role in various fields.

What Exactly Is Standard Deviation?

In simple terms, standard deviation measures the spread of numbers in a dataset. It tells us how much individual data points differ from the mean (average) of the set. If the standard deviation is small, the data points are closely clustered around the mean. If it's large, the data points are spread out, showing greater variability.

Imagine a classroom of students. If most of them score around 80 on a test, with a few scoring slightly higher or lower, the standard deviation will be small. However, if the scores are all over the place—some students scoring 40, others 90—the standard deviation will be large, indicating a greater spread of scores.

In a nutshell, standard deviation gives us insight into the consistency or variability of data.

How Is Standard Deviation Calculated?

The standard deviation calculation follows a few straightforward steps. Here's a breakdown:

Find the Mean: First, calculate the average (mean) of the dataset by adding up all the values and dividing by the number of values.

Calculate Each Deviation from the Mean: Subtract the mean from each data point to find how much each one differs from the average.

Square Each Deviation: To avoid negative values canceling each other out, square each deviation from the mean.

Find the Average of These Squared Deviations: Add up the squared deviations and divide by the number of data points (or, in some cases, by the number of data points minus one for a sample).

Take the Square Root: Finally, take the square root of this average to get the standard deviation.

The result is a single number that summarizes the overall spread or dispersion of the dataset.

Why Is Standard Deviation Important?

Now that we've discussed how standard deviation is calculated, you might wonder: why is this number so important? The importance of standard deviation lies in its ability to provide context for data. Here's why it matters:

1. It Measures Variability

At its core, standard deviation gives us an understanding of variability. In any dataset, whether it's student test scores or daily temperatures, variability helps us understand how spread out the data is. A low standard deviation means the data points are very similar, while a high standard deviation indicates that they differ significantly from one another.

Understanding variability is crucial for making informed decisions. For example, if you're comparing two sets of test scores, knowing the standard deviation helps you see if one set has more consistent results than the other.

2. It Helps Identify Outliers

Standard deviation also helps in identifying outliers—data points that are much higher or lower than the rest of the data. In some cases, these outliers might signal a problem that needs addressing, such as an error in data collection. In other cases, outliers may represent important trends that need further investigation. Either way, standard deviation is a key tool for spotting unusual data points that merit a closer look.

3. It's Used in Risk Assessment

One of the most significant applications of standard deviation is in finance, where it's often used to assess investment risk. A high standard deviation in the returns of a particular stock or investment means its returns vary significantly from the average, indicating higher risk. Conversely, a low standard deviation suggests more predictable, stable returns. Investors use this information to make decisions based on their tolerance for risk.

4. It Plays a Role in Quality Control

In manufacturing, standard deviation is vital for maintaining product quality. Companies often monitor the standard deviation of key measurements to ensure products stay within acceptable limits. If the standard deviation becomes too large, it may indicate problems with the production process, prompting further investigation and adjustments. By keeping standard deviation low, companies can ensure their products are consistent and reliable.

5. It Aids in Data Comparison

Standard deviation makes it easier to compare different datasets. For example, if you're comparing two schools' test scores, the mean alone won't tell you everything. Two schools could have the same average score, but vastly different levels of variability. One school might have students clustered tightly around the average, while the other has students performing all over the spectrum. Standard deviation helps you see this more clearly, offering a fuller picture of the data.

6. It's Fundamental in Probability Theory

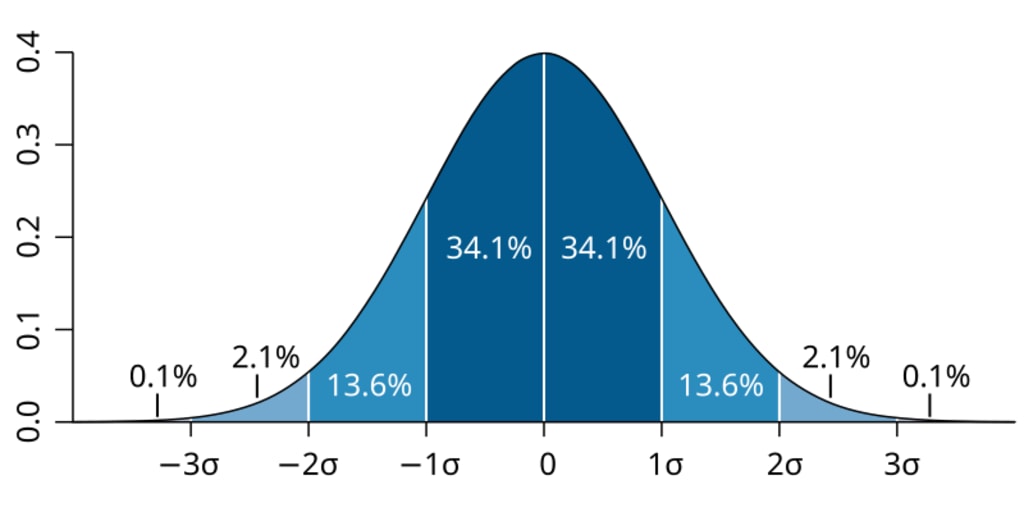
In probability theory, standard deviation plays a crucial role in describing the distribution of data. The most common distribution, the normal distribution, is centered around the mean, with data points spreading out symmetrically. In this context, standard deviation tells us how much data is expected to fall within certain ranges. For example, in a normal distribution, about 68% of the data falls within one standard deviation of the mean, while 95% falls within two standard deviations.

7. It Provides Context for Averages

While the mean gives us an overall picture, it doesn’t always tell the full story. Imagine two sets of data with the same mean but very different standard deviations. One might show little variation, while the other could have a wide spread of values. Without standard deviation, you might miss out on important details about how consistent or variable the data really is.

8. It Enhances Predictive Modeling

In fields like machine learning and data science, standard deviation plays a critical role in predictive modeling. Understanding the variability of data can help refine models, allowing for better predictions and more accurate outcomes. For example, high standard deviation in data can alert data scientists to potential noise or anomalies, prompting them to adjust their models accordingly.

When to Use Standard Deviation

Standard deviation isn't just for statisticians—it's used across industries and fields to understand data better. You might encounter it in:

Finance: To assess the risk of investments

Healthcare: To analyze patient outcomes or treatment effectiveness

Manufacturing: For quality control and consistency checks

Education: To compare student performance across different groups

Weather Forecasting: To measure variability in temperatures or rainfall

Anytime you're dealing with data that has variation, standard deviation can be a useful tool for gaining insight.

Conclusion

Standard deviation is a powerful statistical tool that helps us understand variability in data. Whether you're comparing datasets, assessing risk, or identifying outliers, this simple calculation provides meaningful insights that go far beyond the average. In a world full of data, knowing how to use standard deviation can help you make more informed decisions, leading to better outcomes in everything from investing to quality control.

By recognizing the importance of standard deviation, we gain a better understanding of data's consistency, reliability, and overall behavior—key elements in a wide range of applications. Whether you're working with numbers every day or just trying to make sense of statistics, standard deviation offers a deeper layer of understanding, helping you interpret data in a more meaningful way.